Summer 2018

Project 1 – Analysis of heat shock proteins in Bluegill Sunfish (LepomisMacrochirus)

Faculty Advisors:

• Dr. Eric Guisbert & Dr. Karen Kim Guisbert (Biological Sciences)
• Dr. Munevver Mine Subasi (Mathematical Sciences) & Dr. Ersoy Subasi (Systems Engineering)

BioMath REU Participant:

• Sabrina Perez

Project 2 – Human Impacts on Diatoms Assemblages in an Amazonian Lake over the last 2300 years

Faculty Advisors:

• Dr. Mark Bush (Biological Sciences)

BioMath REU Participant:

• Wuraola Ogundele

Project 3 – Isolation of a Quorum Sensing Regulator in Chlamydomonas reinhardtii 

Faculty Advisors:

• Dr. Andrew Palmer (Biological Sciences)
• Dr. Munevver Mine Subasi

BioMath REU Participant:

• Kirstin Cutshaw

Project 4 – Identification of Signaling Molecules in Starfish Eggs through Bioinformatics

Faculty Advisors:

• Dr. David Carroll (Biological Sciences)

BioMath REU Participant:

• Jamie Kitson-Finuff

Summer 2016

Project 1 – Estimating the Mechanical Properties of Lytechinus variegatus Eggs through Membrane Blebbing

Faculty Advisors:

• Dr. David Carroll (Biological Sciences)
• Dr. Jian Du (Mathematical Sciences)

BioMath REU Participant:

• Darnell Dinwiddie (Biological Sciences)
• Emily Williams (Mathematical Sciences)

Project 2 – Identification of Factors Related to Rapid Progression of Chronic Kidney Disease

Faculty Advisors:

• Dr. Munevver Mine Subasi (Mathematical Sciences)
• Dr. Kristin Pruett (Biological Sciences)

BioMath REU Participant:

• Katie Carroll (Biological Sciences)
• Emily Cunningham (Mathematical Sciences)

Abstract:

This study integrates the principles of pattern-based classification and Kaplan-Meier survival analysis to identify genes and clinical features associated with the rapid progression of chronic kidney disease. The methodology successfully determines the gene-gene survival interactions in the African-American Study of Chronic Kidney Disease with Hypertension (AASK) genomic dataset. The results obtained from this study serves as a basis for the future studies on comparison of the disease progression in white patients with that in African-American patients, both those with and those without apolipoprotein L1 (APOL1) high-risk variants.

Publication:

Pattern-based Classification and Survival Analysis of Chronic Kidney Disease
Munevver M. Subasi, Melissa S. Moreno, Travaughn Bain, Megan Moreno, Ersoy Subasi, Katherine C. Carroll*, Emily R. Cunningham* and Michael Lipkowitz.  ISAIM 2016 - International Symposium on Artificial Intelligence and Mathematics, Fort Lauderdale, FL. January 4–6, 2016. *Summer 2015 BioMath REU Interns

Project 3 – Mitotic Index and Proliferation Rates in Two Melanoma Cell Lines

Faculty Advisors:

• Dr. Lisa Moore (Biological Sciences)
• Dr. Jewgeni Dshalalow (Mathematical Sciences)

BioMath REU Participant:

• Grace Meehan (Biological Sciences)
• Elizabeth Spencer (Mathematical Sciences)

Project 4 – Modeling the Deactivation of MAPK in Sea Urchin Eggs

Faculty Advisors:

• Dr. David Carroll (Biological Sciences)
• Dr. Jian Du (Mathematical Sciences)

BioMath REU Participant:

• Chelsea Maceda (Biological Sciences)
• Sage Malingen (Mathematical Sciences)

Project 5 – Effects of Nutrient Scarcity and Kin Recognition on Root Lengths in A Model Angiosperm

Faculty Advisors:

• Dr. Andrew Palmer (Biological Sciences)
• Dr. Nezamoddin Nezamoddini-Kachouie (Mathematical Sciences)

BioMath REU Participant:

• Katelyn Flaherty (Biological Sciences)
• Jonathan Wamsley (Mathematical Sciences)

Other Proposed Projects

Project 1 – Understanding Island Adaptation of Song Sparrows Using Genomic and Bioinformatics Tools

Faculty Advisors:

• Dr. Christin Pruett (Biological Sciences)
• Dr. Munevver Mine Subasi (Mathematical Sciences)

Island populations have been called “nature’s test tubes” (Losos and Ricklefs, 2009) because they are particularly amenable to examining patterns of evolution. Since Darwin's seminal book (1845) researchers have noted traits that are shared among many island taxa including gigantism, loss of flight, and tameness that are thought to be the result of strong selective pressures (Grant, 1998). Only recently, with the advent of next generation sequencing approaches and the subsequent development of bioinformatics tools, have researchers begun assessing the genetic basis of adaptation (Deagle et al., 2013). We will examine the genomics of song sparrow (Melospiza melodia) populations using 1,000 SNPs identified as being possible candidate markers for island adaptation in this species (Srivastava et al., 2012). Song sparrows found in the Aleutian Islands of Alaska exhibit several traits associated with island adaptation not found in mainland populations including gigantism (Fig. 1) and loss of migratory behavior (Pruett and Winker 2005). We will compare island and mainland locations and two closely related species (Melospiza georgiana and Melospiza lincolnii) to identify loci that are likely to be under selection in island populations. Identified loci will then be compared with the zebra finch (Taeniopygia guttata) and the forthcoming song sparrow genomes to map the locations and function of these regions. The genetic data for this project is in hand.

Proposed Research Activity: The biggest challenge encountered in the analysis of SNPs data is to decide which and how many SNPs (or genes in a microarray data) should be selected for further studies. In this project students will develop systematic procedures that take advantage of computer-related developments and advanced combinatorial optimization techniques for optimizing feature selection in the song sparrow SNPs data and for identifying the set of combinatorial patterns of SNPs that distinguish island sparrows from mainland populations. Students will be exposed to traditional statistical methods and more sophisticated techniques including support vector machines (Burges, 1998; Schölkopf, 2002), decision trees (Quinlan, 1993), neural networks (McCulloch, 1943; Minsky, 1969; Rumelhart et al., 1986), logical analysis of data (Hammer et al., 1986, 2006; Alexe et al., 2003-2006; Reddy et al., 2008; Subasi et al., 2012, 2013), and emerging technologies such as web services and grid computing. Ultimately, loci identified as being functionally important in island adaptation will be examined in other species of birds in the Aleutian Islands that also exhibit gigantism (Gibson and Byrd) such as rock ptarmigan (Lagopus muta), common raven (Corvus corax), and Pacific wren (Troglodytes pacificus).

Project 2 – Coral Reef Growth: Past, Present, and Future

Faculty Advisors:

• Dr. Robert van Woesik (Biological Sciences)
• Dr. Nezamoddin Nezamoddini-Kachouie (Mathematical Sciences)

Coral reefs support the most diverse marine assemblages on Earth. Not only are coral reefs spectacularly beautiful systems, they also provide food resources and environmental services. Indeed, coral reefs provide fishes for millions of people living adjacent to reefs, but they also act as barriers that protect island nations from large-storm waves. The recent increase in CO2 in the atmosphere, however, through the high emission of fossil fuels has increased the temperatures of the atmosphere and increased the temperatures of ocean surface waters. In combination these temperature increases are increasing global sea level. Island nations are particularly vulnerable to such climate change, particularly islanders that live less than 1 m above modern sea level. Over the next century, the climate is predicted to drive water temperatures even higher than today, and considerably above temperatures experienced by reef corals for over the last 700,000 years. Whether coral reefs can ‘keep up’ with continued sea-level rise is largely dependent on i) future rates of sea-level rise, and ii) future responses of reef growth in a warmer ocean. Therefore the key research question here is: where will coral reefs continue to thrive and be able to keep up with sea-level rise in a warming ocean? This project will examine and develop new models of coral-reef growth.

Coral reefs have in the past been able to keep up with sea level rise; if a reef is depauperate of corals it will not be able to keep up with sea level rise. We will consider and model whether reefs can ‘keep up’ with predicted sea-level rise in the near future. We will compare estimated vertical extension rates with rates of sea-level rise under four representative concentration pathways. Coral-reef growth can be considered as a simple system of reef growth minus erosion. Through geological time, reef growth has only occurred when the local production of calcium carbonate exceeds the local destructive processes. Production depends on the densities of organisms that are able to accrete calcium carbonate; whereas destructive processes are a function of the rates of biological, physical, and chemical erosion. We will try and capture the main processes that are involved in coral-reef growth and model the system and predict rates of change. These growth rates will be compared with global climate models that predict changes in ocean temperature and sea-level rise.

Student outcomes

Students will have the opportunity to develop their methods in a modern computing environment at Florida Institute of Technology. First students will learn standard statistical analysis techniques using R, and will develop new methods to investigate the relationship between modern and past coral-reef processes. The students will then investigate potential reef-growth models and predicted climate change predictions. The problems will be addressed through team discussion, experimental design, and study of the existing methods. Students will also participate in discussions to address how the findings can be used toward development of new generation of applications. They will also practice how to share their ideas, think analytically, and go through the decision making process as a team. This project would provide them a balanced combination of theoretical study, practical algorithm design, and teamwork. 

Sea level changes

Changes in sea level are a direct consequence of ice ages; during an ice age large water masses are stored as ice at the poles. There were no major ice ages before the Pleistocene epoch (1.6 my BP) because the world was probably too warm to be easily pushed into an ice-age. The earth cooled through the Cenozoic era (65 my BP) and at the start of the Pleistocene was ready to freeze. The Pleistocene was colder than today, and every now and then was nudged into glaciation due to fluctuations in the path and position of the earth. Changes in the Earth's position relative to the sun have profound effects on the earths climate, and may indeed provide the final push toward ice ages.

The earth's relationship with the sun changes in 3 ways: (1) in its orbit (eccentricity, or the path it follows around the Sun in 1 year), the elliptical circuits vary in shape, sometimes the ellipse is almost a circle (cycle from circle to ellipse is 95,800 years); (2) in its tilt (inclination, or obliquity -the angle of its axis of spin), it varies from 21.39o to 24.36o (cycle 41,000 years); (3) and in its precession (or wobble), a wobble is approximately 21,700 years.(1) In total these three effects are called Milankovich cycles (after Milutin Milankovich in the early twentieth century). The constant flipping from ice age (glacial) to interglacial throughout the Pleistocene is related to the Milankovich cycles. These cycles are roughly 100,000 years.

Moreno glacier, Patagonia, South America (photo by Col Whittingham)

Ice ages and consequences

Ice ages cause drops in what is referred to glacio-eustatic sea levels (where eustatic is a term used to define a global effect). During these times sea level can drop as much as 130 m during the glacial maximum. Recently, McCulloch et al. (1999) established that the sea surface temperature of tropical Indo-Pacific water, more specifically around Papua New Guinea, in the penultimate (i.e., one before the final) deglaciation period (1300,000 years ago), when sea level was 60 m below today's level, was approximately 7 degrees Celsius lower on average than it is today (at 29oC). When sea levels rise, because of ice cap melting, two lots of non-concurring models suggest what happened next. The first model argues for a gradual rise (Bloom, Chappell and Shackleton 1986), and the second model suggests a two-step process (Fairbanks 1989). Fairbanks argues that deglaciation occurred with maximum melting rates from 14,000 to 12,000 years BP, and from 10,000 to 7,000 years BP separated by a mid-deglacial pause with no ice loss (Fairbanks 1989). It appears that Fairbanks was right.

The rise in sea level is generally referred to as the transgression (when sea level falls it is classified as the regression), that only occurs during an inter-glacial period as we have today. The transgression allowed seas to again inundate the continental shelves from their low stand. The geological period in which the transgression occurred is called the Holocene (or recent) and began some 10,000 years ago. It stabilised to modern level at around 6 000 years BP, but slowly rose +1.5 m around 2 500 years BP and quickly subsided again to modern levels.

Geology and Geomorphology

This essay does not cover types of reefs, for that information see Hopley (1982). With a rising sea level, coral reefs started growing during the onset of the transgression over antecedent foundations (old reef structures), or karsts. The reefs we see today are built in the Holocene, but many are merely a veneer covering old reefs that were deposited in earlier times (for example during the Pleistocene). Most coral reefs growing today are growing on substrates that stood above sea level many times throughout the Pleistocene(2).

Early reef growth through the transgression produced "juvenile" reefs, growing toward sea level. They evolved through vertical growth to form "mature" reefs, with reef flats at modern sea level. Further infilling of reefs with lagoons occasionally terminated their growth; these reefs are typically referred to as "senile" reefs. The two most important parameters(3) determining reef morphology are (1) the morphology and depth of the pre-Holocene reefal surface; (2) the net rate of reef accretion (Hopley 1983). Prior to Hopley's paper in 1983 reef morphology was thought to be largely a consequence of the molding action of wind, waves and currents. This may indeed be the case once the reef has reached sea level, however other factors are dominant before this stage.

Reef variation

We will briefly examine the Great Barrier Reef (GBR) as an example of the general variation in reef development. In the GBR region, outer reefs, that are exposed to high wave energy regimes, tend to be framework reefs supporting mainly framework corals (branching and massive), whereas the inner reefs tend to more detrital (composed of rubble, sand and mud). Outer reefs also have much higher levels of cementation (by coralline algae), whereas the inner reefs have virtually none.

Inshore fringing reefs are common on many continental islands close to the mainland shore. The best developed of these reefs typically have both framework and detrital elements and distinctive reef flats and reef slopes. The least developed are termed 'incipient reefs, essentially detrital banks without reef flats, that are colonised by hard corals, and usually with other sessile benthos such as macro-algae, soft corals and zoanthids. In addition, there are coral communities without appreciable framework or detrital accumulations on the rocky flanks and headlands of the islands.

For many Great Barrier Reef reefs, reef growth commenced between 8,320 and 7,500 y BP (Hopley 1982). On many inshore reefs the entire accretion of reef structure has taken place during the last 6,000-5,000 years. A time lag between reef initiation and the transgression may have been due to terrigenous influences and high turbidity on a shallow shelf. Chappell et al. (1983) proposed two models for the development of fringing reefs with reef flats; one for those which had reached their current widths soon after sea level peaked 6,000 - 5,000 y B.P., and one for those whose seaward edge has gradually advanced across the sea floor since that time. In both models, coral growth on the reefs outer margin is a primary source of the skeletal elements comprising the reef matrix. The average growth rate for reefs has been reported at 4-5 mm per year, although incipient reefs grow at a rate of < 1 mm per year.

In the Ryukyus Islands of Japan, Holocene reefs began forming on old carbonate foundations some 8,500 to 8,000 y BP. Research has been undertaken primarily on, Kikai Island, Kume Island, Yoron Island, Okierabu Island, and Minna Island. Kikai Island and Kume Island are uplifted intermittently therefore the story there is more complicated. A typical reef at Yoron Island appeared to have grown at 1-3 mm a year, and reached modern sea level about 5,000 years ago. Holocene deposits range from 3.0 to 15.0 m. Okierabu and Minna are quite contrasting reefs, the former was constructed only by upward growth and reef flat formation, while the latter started as a barrier that later infilled. Therefore, the former is only narrow while the later is quite wide. Reef growth can be divided into three stages: the initial stage of upward growth, the second stage of reef crest formation, and the third stage of formation of other reef features, such as spurs and grooves and reef flats (Kan et al. 1995).

Reef growth

Reef growth through the Holocene has added a veneer to most reefs grown over pre-existing fossil reefs, but have contributed almost entirely to fringing reef growth on the Great Barrier Reef. Differences in degree of coral reef development are a consequence of time-varying differences in the rates of production versus destruction, and of accumulation versus dispersal, (of the skeletons of reef-building organisms,) throughout the time available for the reef to grow. In other words, the process of reef building is by (1) biological accretion (by corals and calcareous algae) and by (2) sedimentological accretion (by deposition of reef associated organisms) and is (3) tempered by destructive processes, such as through the action of parrot fish, echinoids, infaunal sponges and polychaete worms, and by other natural and human impacts. In summary, net reef growth is the sum of framework accretion, sedimentological accretion and destruction.

Framework accretion

Biological coral reef accretion is the consequence of coral and algae growth. This can be described in terms of the demography of calcifying organisms: their densities and frequency of settlement; their rates of growth; their mean longevity's and maximum sizes; their fates following death. The increasing mass and decreasing surface area to volume ratio which accompanies aging of reef building corals are both conducive to retention of large reef building blocks on site, and the progradation of the reef across the sea floor. By contrast, short-lived colonies have a larger surface area to volume ratio at time of death, and are thus more prone to be disintegrated and dispersed by bio-eroders and by breakage, waves and currents. Reefs thus become well developed as a consequence of high settlement densities and great longevity maximising retention of large framework elements on site. They fail to develop or to progress beyond the 'incipient stage, if either or both of settlement densities and longevities are too low to counteract the bioerosional and physical losses.

On any one particular reef there are locations that are either sources or sinks of reef sediment. The outer, windward reef edge is usually the prime source. Lagoons and reef slopes, or sub-tidal and intertidal rubble banks on reef flats, are usual sink locations. At least half of the material initially incorporated in the reef (gross production) may be exported from the reef. On reefs where export is limited the reef may prograde backward by the addition of sand sheets.

"Turn ons" and "turn-offs"

Reef development can be interpreted in terms of 'turn-ons' and 'turn-offs'. Clues to the nature of the turn-on/ turn-off mechanisms may be provided by interpretation of patterns in community structure and the physical environment. Reef growth is 'turned on' where physical conditions are suitable reflected in the high settlement densities of corals, and long individual life expectancies which lead to large colony sizes, especially in massive and branching forms. Here, it appears that individual colonies persist longer and accrete more often into existing framework even in spite of periodic natural perturbations. In contrast, sparsely covered and poorly developed reefs appear to be 'turned off'. This is usually the case in harsh physical environments. The biological community clearly reflects the harsh conditions by showing a high population turnover, high rates of skeletal decay, and a narrow euphotic zone. These factors may combine to limit the accumulation of reef framework and detritus necessary for reef accretion. Fast colony growth may offset negative effects of a sparse and ephemeral coral community in terms of production of reef framework and rubble. However, short life expectancies and low recruitment densities, in combination, are not conducive to the accumulation of a carbonate matrix. Upon death, the small, lightly calcified and poorly cemented skeletons are more prone to disintegration by bio-eroders, and to breakage (Van Woesik and Done, 1997).

Project 3 – Microorganism Motility in Complex Fluids

Faculty Advisors:

• Dr. David Carroll (Biological Sciences)
• Dr. Jian Du (Mathematical Science)

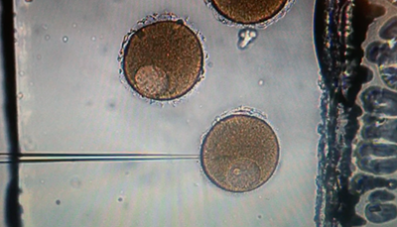The navigation of microorganisms through their fluidic environment is critical for many biological processes. In a successful fertilization, spermatozoa must swim though cervical mucus, as well as eventually penetrate the cumulus layer of the oocyte complex in mammals and in organisms that spawn, the spermatozoa will encounter the different viscosities of sea water and the egg jelly that immediately surrounds the egg (Wassarman, 1987). Disease-causing bacteria such as Escherichia coli and Salmonella typhimurium revolve in intestinal fluids by rotating their helical flagella (Lauga and Powers, 2009). Understanding the physics and biology underlying microorganism or unicellular motility is one of the most important goals in the research of biological physics and cell biology. Recently, further interests have been raised in this area, motivated by the development of individual micro- and nanoscale artificial swimmers for applications including targeted drug delivery and robotic surgery. Swimming problems in a Stokesian Newtonian fluids have been extensively studied and the underlying physics is well understood. On the other hand, many biological fluids with suspended microstructures exhibit complicated non-Newtonian mechanical responses. The fundamental mechanisms of microorganism motility in a complex biological fluid are only beginning to be uncovered. Previous research has treated the polymeric fluid as a single-phase continuous medium. However, for some complex materials, such as gels, there may be relative motion differences between the polymer network and the water, and then single-phase models for such materials may not be appropriate.

Proposed Research Activity: Based on the extensive expertise and previous developments of the group, the proposed REU activities will concentrate on the locomotion problems in complex fluids through a combination of analytical, computational and experimental tools. Specifically, we plan to:

1. Build realistic computational models to simulate the interactions between elastic structures and surrounding gels. Jian Du and colleagues have developed an efficient and robust computational algorithm for multiphase gel dynamics, which is able to handle gels with widely varying rheological properties. They also invented a novel two-phase immersed boundary (IB) scheme using penalty method and successfully simulated swimming problems in mixtures of two viscous fluids. Different boundary conditions will be accounted for in the model. For example, when the polymer is sparse in the swimmer scale, we will use so-called solvent mediated boundary conditions (i.e., zero stress on swimmer). Otherwise, a mechanical slip law will be applied to the boundary. Instead of the IB framework, we will adapt a projection-type method for these more general boundary conditions. Instead of being evaluated from constitutive relations, the boundary forces act as a Lagrange multiplier to satisfy related boundary condition. We expect this improvement will dramatically enhance the computational efficiency. Students will be trained to use this model and learn how it was developed mathematically.
2. Through various experimental methods, students will provide essential input data for the model. For example, the rheological properties of the biological fluids will be measured experimentally. The primary focus will initially be in vitro fertilization using the starfish Patiria miniata as a model. These starfish produce millions of gametes and the process of in vitro fertilization is well established. A layer of egg jelly, which consists of polysaccharides and embedded peptides, surrounds the starfish egg. The swimming behavior of the spermatozoa will be visualized by high-speed video and analyzed. Changes in swimming behavior in the two media will be a focus of the research problem.
3. One of the advantages of the fertilization model is that it will allow us to couple biochemistry with the hydrodynamics model, such as the role of calcium release and the resulting hyperactivation dynamics of the sperm. The sperm morphology is also altered by the acrosome reaction during this process, adding to the possibilities for altering and improving the model.
4. Therefore, students in this laboratory will gain experience in developing and testing complex models of swimming behavior. As data is gathered, they will also be able to input this real information into the model and test how it fits with real biological complexity.

Project 4 – Modeling the Growth of Cancer Cells

Project 5 – Automated image analysis systems with applications to biology: techniques, problems, and impacts